存在性问题之等腰三角形
【例题讲解】

【解析】
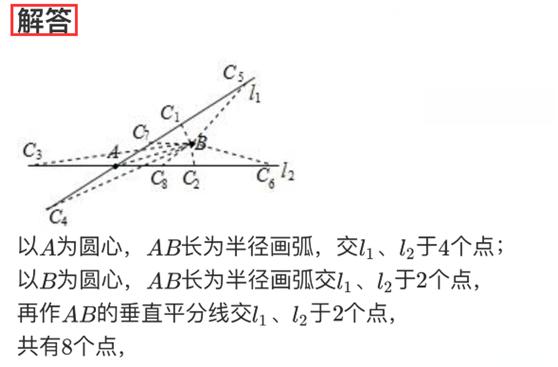
以A为圆心,AB长为半径画弧;以B为圆心,AB长为半径画弧,再作AB的垂直平分线分别找出交l?、l?点的个数即可.
【点评】
此题主要考查了等腰三角形的判定,关键是掌握两边相等的三角形是等腰三角形.


【解析】
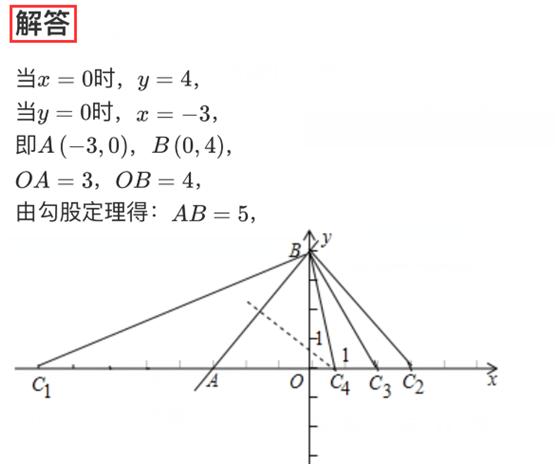
求出A、B的坐标,求出OA、OB、AB的值,有三种情况:①以A为圆心,以AB为半径交x轴于两点,AC=AB=5;
②以B为圆心,以AB为半径交x轴于一点(A除外),AB=BC,OA=OC=3;
③作AB的垂直平分线交x轴于C,设C的坐标是(a,0),AC=BC,求出C的坐标即可.
【点评】
本题考查了一次函数的图象上点的坐标特征、等腰三角形的性质和勾股定理的应用,主要考查学生的分析问题和解决问题的能力,用了分类讨论思想,题目比较典型,有一定的难度.





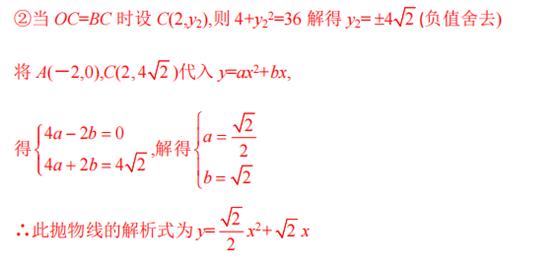
【解析】
(1)过点D作DF⊥x轴于点F,由抛物线的对称性可知OF=AF,则2AF+AE=4①,由DF//BE,得到△ADF~△ABE,根据相似三角形对应边成比例得出AF/AE=AD/AB=1/2即AE=2AF②,①与②联立组成二元一次方程组,解出AE=2,AF=1,进而得到点A的坐标;
(2)先由抛物线过原点(0,0),设此抛物线的解析式为y=ax2+bx,再根据抛物线过原点(0,0)和A点(-2,0),求出对称轴为直线x=-1,则由B点横坐标为-4得出C点横坐标为2,BC=6.再由OB>OC,可知当△OBC是等腰三角形时,可分两种情况讨论:①当OB=BC时,设B(-4,y?),列出方程,解方程求出y?的值,将A,B两点坐标代入y=ax2+bx,运用待定系数法求出此抛物线的解析式;②当OC=BC时,设C(2,y?),列出方程,解方程求出y?的值,将A,C两点坐标代入y=ax2+bx,运用待定系数法求出此抛物线的解析式.
【点评】
本题考查了二次函数的综合题型,其中涉及到二次函数的对称性,相似三角形的判定与性质,运用待定系数法求抛物线的解析式,等腰三角形的性质,两点间的距离公式等知识,综合性较强,难度适中.运用数形结合、分类讨论及方程思想是解题的关键.

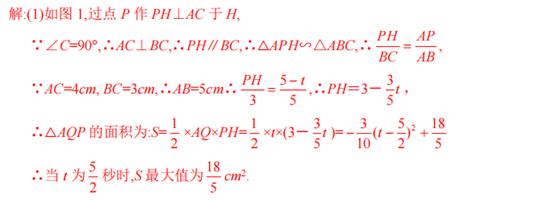


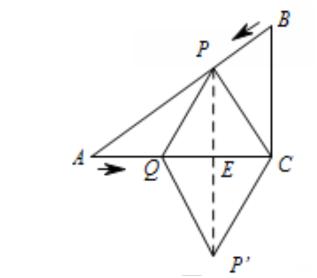





【点评】
此题主要考查了相似形综合,用到的知识点是相似三角形的判定与性质、勾股定理、三角形的面积公式以及二次函数的最值问题,关键是根据题意做出辅助线,利用数形结合思想进行解答.



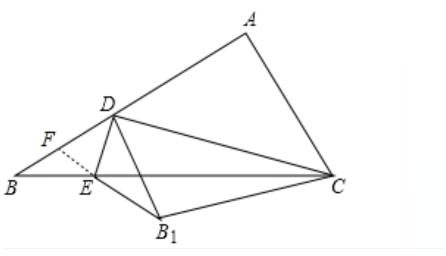
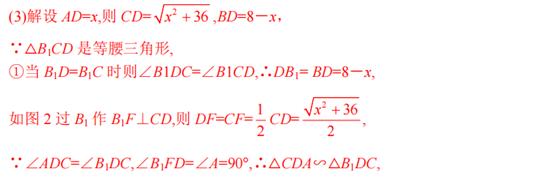

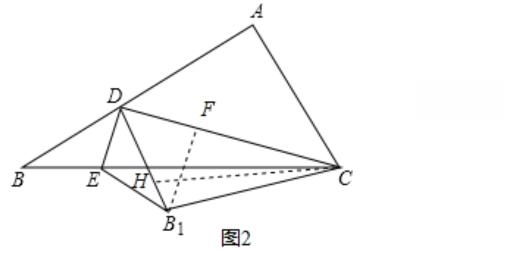


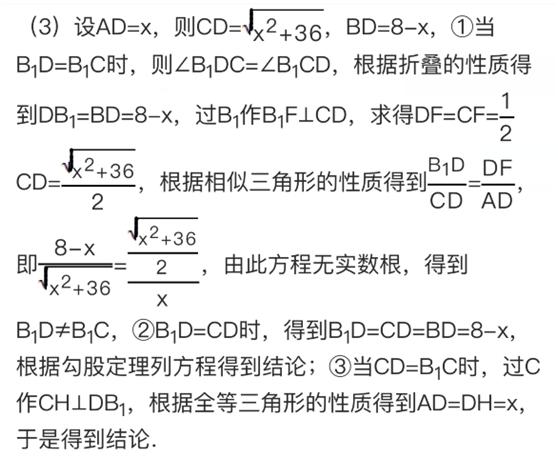
【点评】
本题考查了全等三角形的判断和性质,相似三角形的判定和性质,勾股定理等腰三角形的性质,正确的理解题意是解题的关键.






暂无评论
发表评论